ناصر فروندیان
اگه قبلا با آموزشهای ما همراه بودین، درجریان هستین که جلسه قبلمون در مورد Naked Pair یا جفت آشکار که شاخهای از Subsetها بود آموزش دادیم و گفتیم اگه دو خونه توی یک واحد دو کاندیدای یکسان (Bi Value یکسان) داشته باشن بهشون Pair گفته میشه که اگه آشکار باشن اسمشون Naked Pair میشه و اگه مخفی باشنHidden Pair میشن.
حالا توی این جلسه قراره در مورد سهگانه و چهارگانههای آشکار صحبت کنیم و بحث Naked Subsetها دیگه بسته بشه.
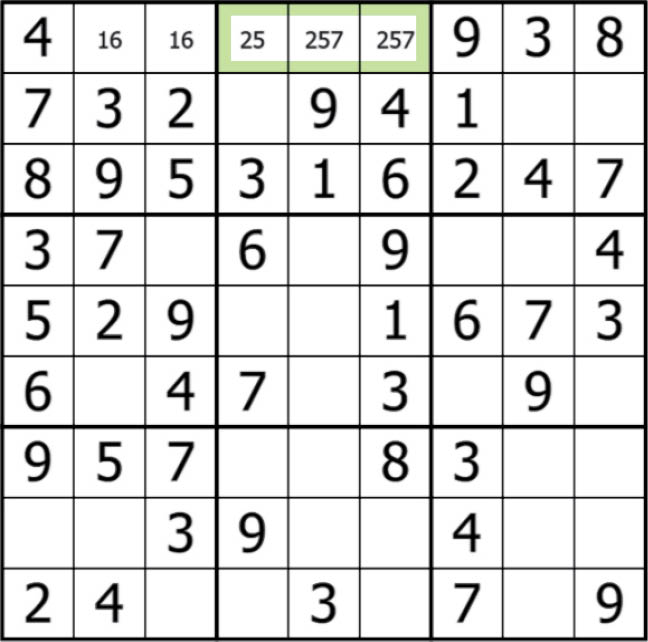
سودوکوی بالا رو جلسه قبلی با هم مرور کردیم و در مورد جفتهای آشکارش با هم صحبت کردیم که چند کاندیدای صحیحش هم سرجاش قرار داده شد.
حالا جا داره یه تعریف جدید رو بهتون معرفی کنم به اسم مجموعههای قفلشده(Locked Sets). ما به تمامی دوگانه، سهگانه، چهارگانه و... که توی سودوکو پیداشون میکنیم به دلیل اینکه توی اون خونهها قفلشدن، Locked Sets یا مجموعه های قفلشده میگیم. البته باید حواسمون باشه که اجازه ندیم تعداد کاندیداهای خونهها کمتر بشه که در این شرایط به مشکل بر میخوریم. یعنی اگه سه کاندیدا برای سه خونه داشته باشیم، کاری نکنیم که دو کاندیدا برای سه خونه برامون باقی بمونه که سودوکومون رو غیرممکن میکنه.
در این جلسه توی همون سودوکو، توی بلوک دوم خونههای 14، 15 و 16، ما سه کاندیدای 2، 5 و 7 رو کاملا آشکار میبینیم. طبق تعریفی که کردیم، میدونیم که اینها از اون دسته از مجموعههای قفلشدهای هستن که سهگانههای آشکار یا Naked Triple صداشون میکنیم. خب در این سهگانه، ما میدونیم که الزاما باید پاسخ یکی از خونهها 2، یکیش 5 و یکیش 7 باشه. با این شرایط الآن پاسخ خونه 24 ما - یعنی تقاطع سطر دوم و ستون چهارم-کاملا واضح شد! کاندیداهای 2 و 5 و7 که جزو سهگانهمون هستن پس نمیتونن در خونه ۲۴ قرار بگیرن. از طرفی توی این بلوک، ارقام 1،3،4،6 و 9 قبلا به صورت قطعی مشخص شدن. پس تنها کاندیدای باقیمونده توی این بلوک برای خونه 24، فقط و فقط میتونه کاندیدای 8 باشه که پاسخ حتمی خونه ۲۴ میشه.
همونطور که سهگانه رو تجربه کردیم، به همین ترتیب اگه ما چهار خونه با چهار کاندیدای یکسان داشته باشیم، به اونها Quad یا چهارگانه میگیم که بازهم با استفاده از همون منطق میتونیم کاندیداهای اضافی رو در بعضی خونهها حذف کنیم و حل سودوکومون رو راحتتر کنیم.
البته به این موضوع هم توجه داشته باشین که همیشه نباید زیرمجموعههای ما بتونن یه چیزی رو حذف کنن! برای درک این موضوع به چهارگانهای که در بلوک پنجم ایجاد شده توجه کنین.
در آخر لازمه اینم در مورد Locked Setها بگم که کوچکترین مجموعه قفل شده میشه: «یک خونه با یک کاندیدا». چون به تعداد یک خونه فقط یک احتمال وجود داره.
اگه سودوکوی بالا رو تا الآن نتونستین حل کنین، فیلم این هفته رو ببینین.

جمعه 23 تیر 1402
کد مطلب :
197262
لینک کوتاه :
newspaper.hamshahrionline.ir/El1JK
+
-
کلیه حقوق مادی و معنوی این سایت متعلق به روزنامه همشهری می باشد . ذکر مطالب با درج منبع مجاز است .
Copyright 2021 . All Rights Reserved

