ناصر فروندیان
اگه آموزش هفته قبلی رو یادتون بیاد، در اولین جلسه گفتیم که سودوکو قانونش میگه: توی هر ردیف، هرستون و هربلوک باید ارقام 1 تا 9 بدون تکرار قرار بگیرن. ضمنا گفتیم که هدف از آموزش سودوکو، اینه که شما بدون پناه بردن به «حدس و خطا» و البته بدون هیچ اشتباهی بتونین یه سودوکوی کلاسیک رو
به راحتی حل کنین.
خب الآن شما میدونین که یه سودوکو، شامل 81 خونه میشه. ما میتونیم خونهها رو از اولین خونه تا آخرین خونه به نامهای ۱ تا ۸۱ شمارهگذاری کنیم و در آموزشمون به همین نامها صداشون کنیم. ولی مشکلی که پیش میاد اینه که مثلا پیدا کردن خونه شصت و هفتم، برامون کمی سخت و زمانبر میشه. برای همینم یه تعریف مناسبتر برای شمارهگذاری و صدا کردن خونههای سودوکو بهتون یاد میدم:
ما توی آموزشمون برای سهولت کار، اول شماره ردیف و بعد شماره ستون رو -پشت سر هم -میگیم. مثلا عدد 82 -بخونیم هشت دو- معنیش در آموزش ما میشه: خونه تقاطع ردیف هشتم با ستون دوم. یا خونه دوم از ردیف هشتم. حتما از آموزش جلسه قبلی یادتون هست که سطرها از بالا به پایین و ستونها از چپ به راست از ۱ تا ۹ نامگذاری شدن.
در سودوکو، اون ارقامی که از قبل مشخص شدن، به ما سرنخی میدن تا بقیه خونههای خالی رو کشف کنیم. در همون نگاه اول، با توجه به قانون اصلی سودوکو، احتمال داره چندین رقم بتونن برای یه خونه مناسب باشن. به تکتک این ارقام، کاندیدای اون خونه میگیم. اگه اون کاندیداها رو کوچیک توی خونهشون بنویسیم، میگیم این خونه رو با کاندیداهای خودش مدادنویسی (Pencil Mark) کردیم. اما چطور باید مدادنویسی کرد؟! به این سودوکو توجه کنین:
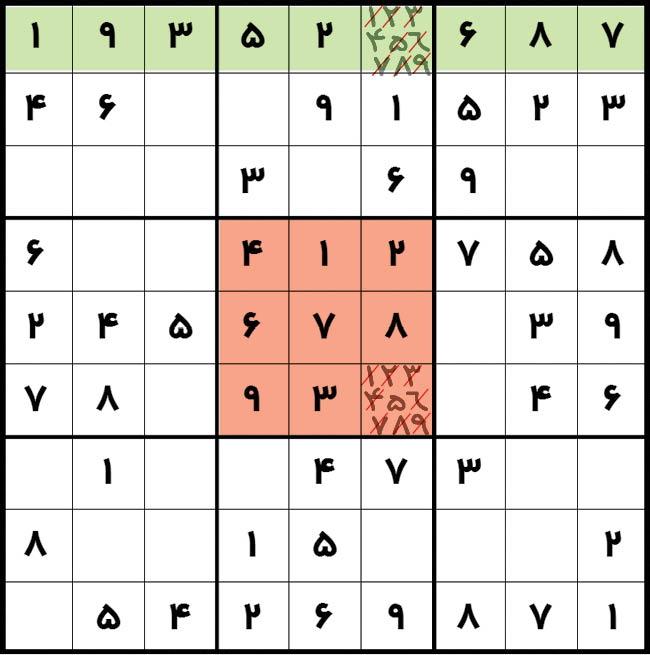
توی ردیف اول یه خونه خالی داریم و اون هم خونه 16 (بخونین یک شش) هستش. یعنی خونه خالیمون در ردیف اول خونه ششم قرار داره. اگه بخوایم این خونه رو مدادنویسی کنیم، باید از 1 تا 9 رو خیلی ریز داخلش بنویسیم و بعدش کاندیداهای اضافی رو با توجه به قانون اصلی سودوکو حذف کنیم. خب متوجه میشیم که خونه 16، فقط و فقط میتونه دارای کاندیدای ۴ باشه چون بقیه کاندیداها با توجه به قانون سودوکو حذف شدن. همین کار رو برای بلوک پنجم - یعنی مربع پُررنگ ۹خونهای وسطی- هم میشه انجام داد. این بلوک هم فقط یه رقم کم داره.
البته خونههایی هم هستن که بیش از یه کاندیدا داشته باشن که پیدا کردن و پُرکردن اونها و نهایتا حل کردن این سودوکوی بسیارساده رو به شما میسپرم.

جمعه 5 خرداد 1402
کد مطلب :
192857
لینک کوتاه :
newspaper.hamshahrionline.ir/y8JBw
+
-
کلیه حقوق مادی و معنوی این سایت متعلق به روزنامه همشهری می باشد . ذکر مطالب با درج منبع مجاز است .
Copyright 2021 . All Rights Reserved



