ناصر فروندیان
سلام. این جلسه قصد داریم نوعی شمشیرماهی یا Sword Fish را با کمی تغییر آموزش بدهیم. شرط برقراری این نوع شمشیرماهی این نیست که سه ردیف و سه ستون متقاطع باشند(با هم ارتباط داشته باشند). شرط این است که سه واحد با هم مرتبط و متقاطع باشند. در تعریف Mutant Sword Fish منظور از «واحد»، همان ردیف، ستون یا بلوک است. به این سودوکوی دقت کنید:
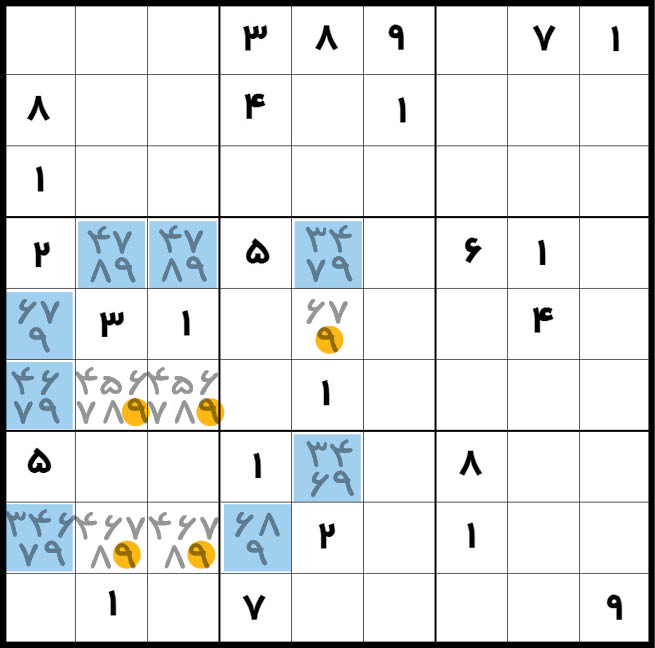
به دنبال کاندیدای 9 هستیم. اول: چون ردیف اول و نهم، ۹ دارد پس در ستون اول تنها احتمالات کاندیدای 9، خانه های آبی هستند. دوم: با توجه به حضور 9 در خانه 99 و 16، بلوک هشتم هم تنها جاهای حضور 9 آبی شد. سوم: حضور رقم 9 طبق سرنخیهایی که داریم، در ردیف چهارم فقط و فقط در خانه های آبی مقدور است. ادعا میکنیم که طبق این حلقه آبیرنگ، میتوانیم تمام کاندیداهایی زرد را حذف کنیم. میپرسید چطور؟!
در بلوک هشتم، یا رقم ۹ در خانه 84 صحیح است یا خانه 75. پس رنگمیکنیم. خانه 84 را بنفش و 75 را سبز می کنیم. حالا که خانه 84 بنفش است باید رقم ۹ بنفشی را برای ستون اول پیدا کنیم. بیشک یکی از دو خانه 51 یا 61 باید بنفش شوند. هر دو را بنفش میکنیم چون نمی توان بهطور قطع گفت کدام باید بنفش باشد. حالا سراغ آخرین واحد(ردیف چهارم)میرویم و از آنجایی که در بلوک چهارم بنفش داریم، پس بیشک خانههای 42 و 43 بنفش نیستند. پس خانه 45 بنفش است. همین کار را برای رنگ سبز خانه 75 هم انجام میدهیم تا به شکل زیر برسیم:
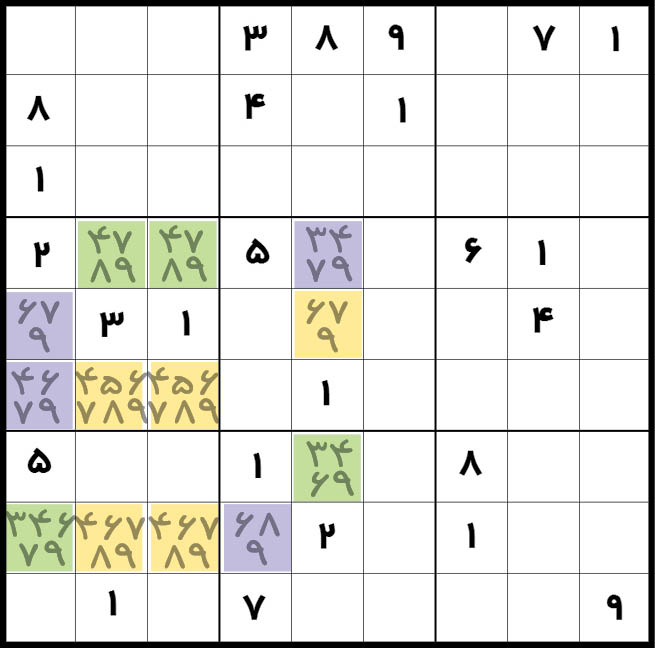
ساده شد! هیچ خانه زردی نمی تواند کاندیدای ۹ صحیحی را داشته باشد! چون یا سبزها باید صحیح باشند یا بنفشها و اگر هریک از زردها ۹ صحیحی داشته باشند، یعنی نه سبزها و نه بنفشها نمیتوانند ۹ باشند. به کمک تکنیک Mutant Sword Fish کاندیدای 9 را از خانه های زرد حذف کردیم. برای خانواده N Fish این را در نظر داشته باشید که به ازای N کاندیدا باید N خانه داشته باشید. در مثال بالا با ۹ شدن هریک از زردها، یکی از واحدها بدون 9 خواهد شد.

جمعه 15 دی 1402
کد مطلب :
214597
لینک کوتاه :
newspaper.hamshahrionline.ir/r0nLE
+
-
کلیه حقوق مادی و معنوی این سایت متعلق به روزنامه همشهری می باشد . ذکر مطالب با درج منبع مجاز است .
Copyright 2021 . All Rights Reserved



