نقش شمشیرماهی‌ها در حل سودوکو!

ناصر فروندیان

سلام. توی این جلسه می‌خوایم در مورد تکنیک دوم خانواده N-Fish که اسمش Swordfish(شمشیر ماهی) هست صحبت کنیم. اولین تکنیک این خانواده N-Fish رو یادتون می‌آد؟ اسمش X-Wing بود. این بار می‌خوایم همون تکنیک رو کمی گسترش بدیم که تبدیل بشه به تکنیک Swordfish. توی تکنیک X-Wing ما  چهار تا خونه داریم که توی دو ردیف  و دو ستون با هم متقاطع باشن.
در اصل، شرط برقراری تکنیک‌های خانواده N-Fish تعداد خونه‌ها نیست، بلکه تعداد ردیف‌ها و ستون‌هایی هستش که کاندیدای ما توش متقاطعه. پس توی تکنیک «شمشیرماهی» کاندیدای مورد نظر ما توی سه ردیف و سه ستون متقاطع حضور داره.
برای درک بهتر تکنیک این جلسه،  به سودوکوی زیر توجه کنین:

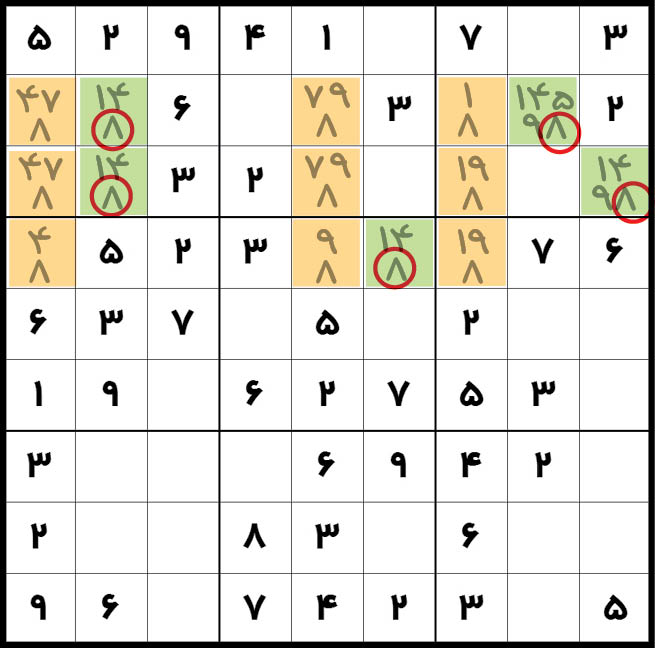
ما توی ستون اول، پنجم و هفتم خونه‌هایی که کاندیدای 8 رو داشتن رو زرد کردیم. این خونه‌ها تنها جاهایی هستن که می‌تونن توی این ستون‌ها، میزبان کاندیدای ۸ بشن. این خونه‌ها با ردیف دوم، سوم و چهارم متقاطع هستن. به این شکل می‌گیم: «شمشیرماهی فرمت 3-3-3»! یعنی توی ستون اول و دوم و سوم هر سه  خونه، کاندیدای 8 داریم.
خب. حالا قبول دارین که ما برای هر ستون، فقط یه کاندیدای 8 نیاز داریم؟ و حتما قبول دارین برای هر ردیف رنگ شده هم فقط یدونه 8 نیاز داریم. پس ما فقط می‌تونیم توی خونه‌های زرد کاندیدای 8 خودمون رو بذاریم. به عبارتی خونه‌های سبز، نمی‌تونن دارای کاندیدای 8 باشن. چرا؟! چون هر یک از این خونه‌های سبز اگه 8 باشن، باعث می‌شن یکی از واحدهای ما بدون 8 باقی بمونه! به زبون ساده‌تر: هر جایی توی این شمشیر ماهی(خونه‌های زرد) کاندیدای 8 بشینه، باعث می‌شه یه X-Wing تشکیل بشه. با همین منطق تمامی کاندیداهای 8 خونه‌های سبز باید از بین برن.
خب حالا بیاین خونه 21 رو دارای رقم قطعی 8 فرض کنیم. پس توی ستون اول و ردیف دوم ما یدونه 8 قطعی داریم و لذا تمامی کاندیداهای 8 که این خونه رو می‌بینن باید حذف بشن.
حالا از زردها چی باقی مونده؟ بله درسته. خونه‌های 35، 37 و 45 و 47 مونده که اگه دقیق بهش نگاه کنین خودش یه  X-Wing شده که باعث می‌شه تمامی کاندیداهای 8 که توی خونه‌های سبز باقی‌موندن هم از بین برن.
من فقط ۸ رو توی یکی از خونه‌های زرد امتحان کردم. شما می‌تونین توی بقیه خونه‌ها آزمایشش کنین و ایکس وینگ‌ها رو پیدا کنین.
گفتیم که فرمت این تکنیک 3-3-3 هستش. یعنی توی هر سه ستون(یا ردیف) ما سه بار حضور کاندیدامون رو داریم. حالا به نظرتون این تکنیک با حضور تعداد کمتری از کاندیداها هم ممکنه کار کنه؟! جواب این سوال مثبته! ممکنه ما با شمشیرماهی‌ای روبه‌رو بشیم که فرمتش 2-2-3 یا 2-3-2 یا حتی 2-2-2 باشه که این 2-2-2 یعنی 6 خونه به جای 9 خونه زردرنگ می‌شن. اما بدونین که در اون شرایط هم ما سه ستون(یا ردیف) داریم و این ستون‌ها و ردیف‌ها هستن که منطق ما رو کامل می‌کنن و نه تعداد خونه‌ها! برای آشنایی با فرمت 2-2-2 پیشنهاد می‌کنم ویدئوی این هفته رو از دست ندین.